Statistical Machine Learning: Difference between revisions
(Added LLM section) |
|||
| Line 215: | Line 215: | ||
Take high throughput data and simplify before work is done ''ex'': 1080p @ 60fps <math display="inline">\rightarrow</math> 240x360 @ 15fps, broken into component channels Gaussian blur filter kernel applied to high-res images Edge detection via double threshold ML or CNN used past this to determine actual features | Take high throughput data and simplify before work is done ''ex'': 1080p @ 60fps <math display="inline">\rightarrow</math> 240x360 @ 15fps, broken into component channels Gaussian blur filter kernel applied to high-res images Edge detection via double threshold ML or CNN used past this to determine actual features | ||
</div> | |||
==== Large Language Models ==== | |||
Large language models (LLMs) are stochastic systems which attempt to capture the 'shape' of a language (a recursively enumerable language by [[wikipedia:Chomsky_hierarchy|Chomsky Hierarchy]]) by pulling successive tokens from a '''bag of words model'''; in this system, a corpus of text is transformed into a mathematical space of the tokens, which are substrings of the input language, and weights, which are a cosine similarity between tokens in a Hilbert space. In other words, a large language model is a function which descends the gradient of this space, and uses probability to arrive at what word goes next in a given completion. This mathematical loss minimization is performed sequentially as the text is generated, in what is known as '''self-attention''', which relates different positions of text sequence in order to compute a representation of the sequence. This function takes the form: | |||
<math display="block">\sum_{t=1}^T P(x_t | \vec{x}_{<t} \vec{x}_{i:j} )</math> | |||
where tokens are generated until limit '''T''' is reached, and where there is a probability of another token generated as a function of previous tokens and the input. This functional setup is called an '''encoder-decoder'''. | |||
So, based on the corpus, and given an input, an encoder-decoder will try to create a response given an input. Usually, encoder-decoders are further trained by a process called '''Reinforcement Learning from Human Feedback''' (RLHF), in which human feedback is given in an iterative process until the underlying language weights prefer the trained preferences. | |||
====== To consider in regard to LLMs: ====== | |||
* They are stochastic word generator machines, and contain structure, rather than problem solving logic. | |||
* They are typically computationally expensive to run. | |||
* They are typically monstrously computationally expensive to train. | |||
* If equipped with enough memory for self-attention, they become a Turing Machine with Type-0 Grammar. | |||
* They may occasionally generate incorrect information. | |||
* They '''hallucinate''', generating nonsense (verbal noise) when confronted with unexpected text not encountered in training. | |||
* Because the attention of a model is limited, LLMs perform badly with large multi-step processes which require dense context.</div> | |||
== Software Toolkit == | == Software Toolkit == | ||
| Line 328: | Line 346: | ||
* rdrr.io - meta-manual lookup and many other tools for R | * rdrr.io - meta-manual lookup and many other tools for R | ||
* swirlstats.com - learn R, in R | * swirlstats.com - learn R, in R | ||
* | * statlearning.com - statistical machine learning coursework | ||
=== Recommended Reading === | === Recommended Reading === | ||
Latest revision as of 11:14, 20 March 2023
Overview
A crash course to enable gentle introduction into the machine learning techniques and its applications into data science.
Topics Covered:
- Basic Concepts
- Data Models
- Machine Learning
- ML Techniques
- Software Toolkit
- Continued Learning
Basic Concepts
Definitions:
- Statistical Machine Learning is a set of tools used to model and understand complex data sets
- Data Science is a set of techniques in computing to support the analysis of data
- Not very useful without some domain knowledge: it is important to know your data.
- Includes analytic techniques:
- descriptive statistics
- data visualization
- statistical machine learning
- neural networks
- actor-environment models
- Also includes computational techniques:
- database administration
- management of information systems
- parallelization high performance computing
Basic Concepts
Knowing your data
Technical definition:
Let represent a number of distinct observations, and let represent a number of predictors Then, our observed data is an matrix with row observation vectors and column predictor vectors .
In addition, we will also have response variable(s) , which is a made up of some -length vectors.
So, our combined dataset consists of
Our Mission: determine relationships between and which are mathematically sound, leading to better understanding
Typically a table has columns as features, rows as entries
Entries might be numeric or categorical.
Data sources are either Structured or Unstructured:
- Unstructured data will require some transformation.
Some data may also be time series taking a sampling of points over time, contributing to a 3-dimensional Data Cub
Several techniques can be used to reduce complex data:
- numeric representation mapping of categorical information into numbers.
- scaling redefine a new range for a predictor vector.
- normalization redefine a predictor by its mean and standard deviation, giving a normal distribution of values.
- dimension reduction lose fine grain of data, but gain understandability.
- feature extraction a data mining technique in which we can generate new predictors from known information
Modeling
What is a model?
Very well-known model: Gravity is a functional model between masses, distances, and force. Statistics definition:
Let each of length , and of length , then for and , there exists a function with a systematic and error term : Why do we even estimate at all? Prediction or Inference
Predictive models create an estimator which we can use to estimate using a sample from a larger population: With error: .
Inference models are primarily interested in how is affected by :
- What predictors associated with response?
- What is the relationship of predictors to response?
- What is the overall nature of relationship between and the predictors.
Signal vs Noise
Consider precision and accuracy.
- Both contribute into data set
noise: variation in data which detracts from constructing information, as opposed to signal–data which is representative of a system under study and contains information.
High signal to noise allows us to minimize reducible error, caused by sampling technique.
Different than irreducible error, created by factors we are not measuring.
Error and Fit
In Modeling In the terms of modeling, precision of a model is referred to variance and the accuracy of a model its degree of bias.
Generally, overly complex models generate high variance, and can over-fit to input data, making the model useless to new data.
Generally, Mean Square Error or MSE, used to determine goodness-of-fit for model calibration: .
Error rate used in classification: .
However for reporting, statistic is more often used, because it gives a value between 0 and 1 useful to determine how much of variance in is explained by variance in :
Example functions relating and :
- A linear function:
- A polynomial:
- A natural function:
- A logistical function:
- A series of nested
ifstatements - A series of differential equations:
Why Machine Learning?
Types of Questions:
- Exact Solution is known normal coding problems, linear models, and classical statistics.
- Exact Solution is unknown, but can be extracted with work work with systems experts and domain knowledge to create code.
- Exact Solution is known, but not yet conveyable ML is useful.
- Exact Solution not known by humans ML and/or Deep Learning needed
Example: consider a prediction of temperature:
- Knowledge Based Models
- Physics and atmospheric science based model.
- Up to differential equations on chaotic systems.
- As fine granularity of prediction increases, number of factors and density of data quickly becomes too much for most humans to consider
- Data Driven Models
- Use ML to provide iterative gain to reduce error
- Known data→model creation→point toward new factors.
- Uses a split in training and testing data, or sum of error to move toward the correct answer.
- Human researchers more free to find more data, improve prediction, develop theories
- Use ML to provide iterative gain to reduce error
Techniques
Machine Learning in General
Supervised Learning: the model estimates, error verifies
- If incorrect, needs user input for correction.
- Example: a computer vision system trained to find features in images via user annotated images.
Unsupervised Learning: Clustering/Grouping of similar items
- Need a similarity measure via feature vectors and ability to adjust weights
- Example: Taste prediction algorithms used in web advertising.
Reinforced Learning Model estimates a sequence of guesses
- Correct if and only if the entire sequence or a parameterized output scoring
- Instant feedback but high compute cost
- Example: Game-play in actor-environment model
Types of Problems and Output
Numeric function maps to and output is in .
Categorization non-orderable sorting
Clustering finding principle ways groups differ
Anomaly Detection finding data points which are out of the ordinary
Actor Models real-time decision making or detailed simulation
Predictive Models
Predictive ML models which are also Linear:
- Utilize a split of training and test data: test-training or -fold cross-validation
- use a function mapping of one or more independent variables to the dependent variables, then re-evaluate to reduce error Includes techniques for mixed model reduction
- Reduction of the number of predictors via Lasso, Ridge, and Elastic Net techniques
Feature-vector based models
Nested if statements try to find decision boundaries by distance between independent data and dependent outcome features have weighted probability most information by Bayesian inference
- Decision Trees can be used to create decision models for linearly separable data effectively a neural network with one neuron
- Random Forest utilizes a number of differently-tuned trees trees provide consensus voting-based approach for non-linearly separable data smaller tree depth typically prevents over-fit
Clustering
Groups data into cluster such that distance within clusters is small, and between differing groups is large
Works with any well-defined "distance" function: Euclidean, Hamming, Inner Product, etc.
k-Means Clustering:
- choose number of clusters randomly distribute points, centroids, into feature space
- divide and classify data by distance to centroids
- move centroids based on center of groups repeats until convergence to some epsilon value
- where points no longer move across iterations
- Goodness of Fit for possible values of , an inflection in overall likelihood ratio given by probability function for set
K-nearest Neighbors:
Creates a probabilistic decision boundary within a feature space between centroids
Unsupervised system to find structures of data works on majority voting system
Gradient Boosting:
System attempts to find the direction and vector of change in a dimensional field, and follow these iteratively to find local extrema.
Most use some Quasi-Newton Method for finding extrema for faster centroid convergence.
Support Vector Machine:
Also known as SVM, applies a classifier into high-dimensional data to split points into groups some use a kernel trick.
Generates the inner product space of two arbitrary-dimensional numeric matrix spaces, showing the shape of data
Genetic Algorithms
Utilize some adversarial scoring method of initially randomized vectors:
- ’survivors’ become the basis of new models similar iterative concept to gradient methods.
- Does not have to understand topology of space requires creator to specify scoring for the machine .
Convolutional Neural Networks:
Utilize iterative scoring between training and testing, along with gradient descent on a number of layered, weighted vectors to extract features from a complex data set.
Vision Systems
Take high throughput data and simplify before work is done ex: 1080p @ 60fps 240x360 @ 15fps, broken into component channels Gaussian blur filter kernel applied to high-res images Edge detection via double threshold ML or CNN used past this to determine actual features
Large Language Models
Large language models (LLMs) are stochastic systems which attempt to capture the 'shape' of a language (a recursively enumerable language by Chomsky Hierarchy) by pulling successive tokens from a bag of words model; in this system, a corpus of text is transformed into a mathematical space of the tokens, which are substrings of the input language, and weights, which are a cosine similarity between tokens in a Hilbert space. In other words, a large language model is a function which descends the gradient of this space, and uses probability to arrive at what word goes next in a given completion. This mathematical loss minimization is performed sequentially as the text is generated, in what is known as self-attention, which relates different positions of text sequence in order to compute a representation of the sequence. This function takes the form:
where tokens are generated until limit T is reached, and where there is a probability of another token generated as a function of previous tokens and the input. This functional setup is called an encoder-decoder.
So, based on the corpus, and given an input, an encoder-decoder will try to create a response given an input. Usually, encoder-decoders are further trained by a process called Reinforcement Learning from Human Feedback (RLHF), in which human feedback is given in an iterative process until the underlying language weights prefer the trained preferences.
To consider in regard to LLMs:
- They are stochastic word generator machines, and contain structure, rather than problem solving logic.
- They are typically computationally expensive to run.
- They are typically monstrously computationally expensive to train.
- If equipped with enough memory for self-attention, they become a Turing Machine with Type-0 Grammar.
- They may occasionally generate incorrect information.
- They hallucinate, generating nonsense (verbal noise) when confronted with unexpected text not encountered in training.
- Because the attention of a model is limited, LLMs perform badly with large multi-step processes which require dense context.
Software Toolkit
Python
General purpose programming language with many libraries Interpreted language: each line is run one at a time by a virtual machine.
Dependency Structure
system vs user python
virtualenv: $ python3 -m venv /path/to/new/environment
pip libraries $ pip list outdated format=freeze | grep -v | cut -d=" " -f1 | xargs -n1 pip install -U
Anaconda
separate virtualenv system specifically for data science:
- Spyder IDE with visual output
- JupyterLabs notes with data visualizations
- Orange visual IDE for stats exploration
pandas, NumPy, and SciPylibraries for data serialization and numerical work in pythonmatplotlibfor data visualizationscikit-learnmain library for MLDASKdistributed abstraction layer withpandasgrammar to easily distribute python tasks into 1-1000 compute nodesPyTorch, and TensorFlowdeep learning and CNN generation systems massive compute overhead to train models require data map reduction and or imputation to run well
R language
Statistical programming language: interpreter invokes compiled C or FORTRAN.
Also works within Jupyter notebook for instant visualization, if wanted.
Open-source and extended by the Comprehensive R Archive Network (CRAN), which includes extensive documentation.
rmarkdownformat a document from R with optional LaTeXbindingstidyversedplyrgrammar for mass data manipulationggplot2a library for creating graphs and visualizations
doparallelcost-free abstraction, pooling of CPU threadsmlrinterface to a large number of classification and regression techniquesshinyprovides ability to create web servers similar to NodeJS or Python Flaskl
Intel MKL (Math Kernel Library)
Improves performance for Fast Fourier Transforms, linear algebra operations, vector math, deep neural networks, and kernel solvers.
Default math backend for NumPy, SciPy, and MATLAB
Not hardware agnostic: chooses slowest solvers for non-Intel chips by default
OpenBLAS and LAPACK
LAPACK (Linear Algebra PACKage) provides APIs much like MKL
OpenBLAS (Basic Linear Algebra Subprograms) extends LAPACK with optimizations for parallel computing
Default for R and Biopython
Message Passing Interface (MPI)
Supported by all major compilers (Intel and OpenMP implementations)
An API supporting shared-memory multiprocessing provides backend for many parallel computing systems, allowing for multi-threaded access
ex: mpirun -np $NUM_PROC /path/to/coolProgram < $INPUT > /path/to/output
GNU Parallel
simple vectorization of loops over processors for non-multithreaded processes
ex: parallel -j $NUM_PROC /path/to/thescript.sh ::: 1..n ::: 1..m
CUDA/OpenCL
Nvidia-specific CUDA and open-source OpenCL provide a hardware abstracting API for using GPU for compute tasks
must-have for Pytorch or TensorFlow workloads
Nomenclature Divergence
- CUDA thread = OpenCL work item = CPU lane
- CUDA multiprocessor = OpenCL compute unit = CPU
High Performance Computers
HPC or super-computing clusters provide high throughput analysis.
Amazingly high amount of computational power.
Need to plan your analysis.
NDSU Center for Computationally-Assisted Science and Technology (CCAST) provides a platform for these workloads connect via ssh uses loadable modules:
- ex:
module load parallel
batch processing via PBS scripting
Continued Learning
General Programming/Computers Websites
- StackOverflow.com - check before asking new questions
- RosettaCode.org - data structures and algorithms in many languages
- Linux.die.net/man/ - the Linux manual
- grymoire.com/Unix/ - more *nix CLI tutorials
Python
- docs.python.org/3/ - the official python documentation
- docs.python.org/3/tutorial - the official tutorial
- diveintopython.net - guided tutorial online
- pythontutor.com - visual debugger
R
- cran.r-project.org - CRAN
- cran.r-project.org/manuals.html
- rdrr.io - meta-manual lookup and many other tools for R
- swirlstats.com - learn R, in R
- statlearning.com - statistical machine learning coursework
Recommended Reading
- An Introduction to Statistical Machine Learning by Gareth James et al.
- A Primer on Scientific Programming with Python by Hans Petter Langtangen
- R for Data Science by Wickham and Grolmund
 high performance computing
high performance computing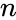 represent a number of distinct observations, and let
represent a number of distinct observations, and let  represent a number of predictors Then, our observed data
represent a number of predictors Then, our observed data  is an
is an  matrix with row observation vectors
matrix with row observation vectors  and column predictor vectors
and column predictor vectors  .
.
 , which is a made up of some
, which is a made up of some ![{\displaystyle [({\vec {x}}_{1},{\vec {y}}_{1}),({\vec {x}}_{2},{\vec {y}}_{2}),...,({\vec {x}}_{n},{\vec {y}}_{n})]}](https://wikimedia.org/api/rest_v1/media/math/render/png/2fcd997136a1692e7f1abc8bb744dddd71da4dd8)

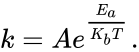 Statistics definition:
Statistics definition:
 each of length
each of length  of length
of length  and
and  , there exists a function with a systematic
, there exists a function with a systematic  and error term
and error term  :
:  Why do we even estimate
Why do we even estimate  which we can use to estimate
which we can use to estimate  With error:
With error: ![{\textstyle E(Y-{\hat {Y}})^{2}=[f(X)-{\hat {f}}(X)]^{2}+\varepsilon }](https://wikimedia.org/api/rest_v1/media/math/render/png/5538d6bdaf99e2cc10e180cf10f3fc1af4d3fb7a) .
.
 .
.
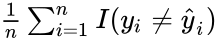 .
.
 statistic is more often used, because it gives a value between 0 and 1 useful to determine how much of variance in
statistic is more often used, because it gives a value between 0 and 1 useful to determine how much of variance in 





 .
.
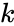 -fold cross-validation
-fold cross-validation possible values of
possible values of  centroids
centroids
